Friedel Weinert

Technological Applications of the Theory of Relativity

1. Introduction.

The 20th century saw the birth of two famous theories: relativity and quantum theory. This article deals with the theory of relativity, which was developed by Albert Einstein (1879-1955) in two stages. In 1905 Einstein proposed his Special Theory of relativity. It is called ‘special’ because it is restricted to uniform motion. That is, either rest or constant motion. Out of this Special Theory grew the most famous equation of all of physics: E=mc². In 1916 Einstein went a step further and proposed his General Theory of Relativity. This theory was no longer restricted to uniform or inertial motion. It applies to both uniform and non-uniform motion. Non-uniform motion occurs when a system undergoes acceleration or rotation. Gravity, for instance, accelerates objects toward the Earth. The General Theory is truly revolutionary because it replaces Newton’s theory of gravitation by the notion of space-time curvature. The mathematics of the General Theory is also vastly more complicated than that of the Special Theory. This article is not be concerned with the mathematical or philosophical aspects of the Theory of Relativity, but with its technological applications. It may not be obvious to the reader but both theories have led to many technological innovations, which are encountered in daily life, from cell phones to GPS, from speed guns to nuclear power. As Atkins put it Einstein “moved civilization forward in two steps.”[1] It is convenient to start with the applications of the Special Theory of Relativity (STR) before turning to the General Theory of Relativity (GTR).

2. Technological Applications of the Special Theory.

From a historical perspective, the Special Theory is basically the crowing of classical physics. But it has vast implications for our understanding of space and time. That is, it affects the measurement of spatial and temporal intervals. In particular, the running of clocks lies at the root of the technological application of the Special Theory.

2. 1. One of the great pleasures of modern life is the freedom of movement afforded by the use of motor vehicles. But as so often there is a sting in the tail. Modern cars can move very fast, and often people break speed limits, resulting in fines. But how is the speed of objects, such as a car or a tennis ball, measured? Speed guns use the so-called Doppler Effect to perform measurements. The effect is named after the Austrian physicist Christian Doppler (fig. 1).

Doppler discovered how the observed frequency of sound waves is affected by the relative motion of the source (for instance, a car) and the detector (ears, speed guns). “Legend has it that he grasped the phenomenon thanks to a type of tuba.”[2] Hence, the effect was known well before Einstein developed his Theory of Relativity. The siren of an ambulance, for instance, has a higher pitch (or frequency) when it is approaching than when it is receding (fig. 2) (Frequency is the number of wave crests that pass a certain point at a particular moment).

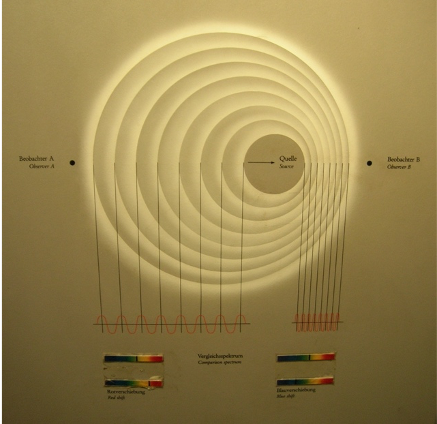
How does this classic Doppler Effect work? Speed guns send out a narrow radio signal, which bounces off the moving car and returns it to the gun. From the Doppler Effect it follows that there is a difference in the frequency, f, between the emitted and the reflected signal. When a car approaches the radar, the frequency of the reflected radio signal is higher than that of the emitted signal. That is, the waves of the returning signal are more tightly packed together than the waves of the emitted signal. From this information, the speed of the approaching car can be calculated (fig. 2).

Doppler’s publication, which described the discovery, was entitled Über das farbige Licht der Doppelsterne (Concerning the Coloured Light of Double Stars). The title indicates that “Doppler extrapolated this phenomenon to light” for it contains a hypothesis about the behaviour of light waves.[3] The frequency of sound waves reflected by a moving vehicle varies with respect to a stationary observer, as has just been observed. So by analogy, Doppler theorized, the colour of light coming from a distant star should change, depending on whether the star moves towards or away from the Earth. Doppler was right but for light waves the theory of relativity has to be taken into account. Sound waves travel only through air but light waves propagate through empty space. Their speed also differs: sound waves travel at approximately 300 metres per second, whilst light propagates at 300,000 kilometres per second. The Doppler Effect for sound waves is therefore different from the Doppler Effect for light waves.

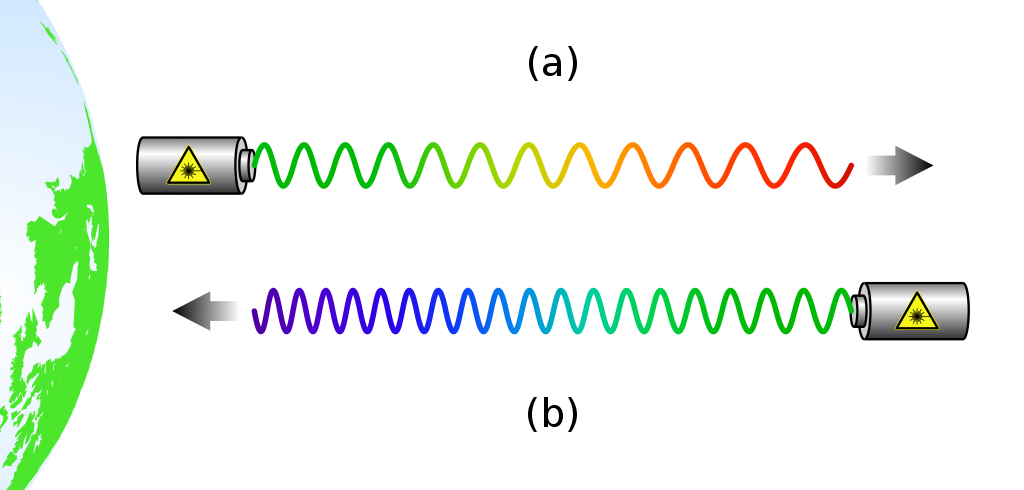
Astronomers use the Doppler Effect to determine the speed of approaching or receding distant stars and galaxies (fig. 3). This situation, however, is not as simple as the case of an approaching fire engine. What has to be taken into account is the fact that light travels at a constant speed of approximately 3×10⁸ metres per second. In his Special Theory Einstein made the speed of light, c, a postulate, which means that no material particle can travel faster than light. [The letter c is used in physics as a symbol for the speed of light. “It has this unsuspected letter for its name probably out of homage for the period before the mid 1600s when science was centered in Italy, and Latin was the language of choice. Celeritas is the Latin word meaning “swiftness” (and the root of the word celerity).”[4] In fact, no material particle can reach the speed of light although it is typical for subatomic particles to be accelerated to up to 99% of c. Over vast galactic distances it takes time for light to be registered on Earth. For instance, radio signals from Mars need 11 light seconds to reach detectors on Earth. And light signals travel for 2 million light-years from Andromeda, our galactic neighbour, before they reach Earth.

Nevertheless, the same principle applies: when a star approaches the Earth its light is shifted towards the blue spectrum (higher frequency); when it recedes from the Earth the light is red-shifted (lower frequency). This has no immediate effects on our daily lives. But it helped astronomers to infer from the data the so-called Big Bang. In 1929 the American astronomer Edwin Hubble (1889-1953) observed the recession of galaxies. It implied that the universe was expanding. If galaxies were receding from view, hence red-shifted, they must have been closer together at an earlier time. Working their way backwards, cosmologists postulated that our present universe originated in a Big Bang some 13.7 billion years ago.

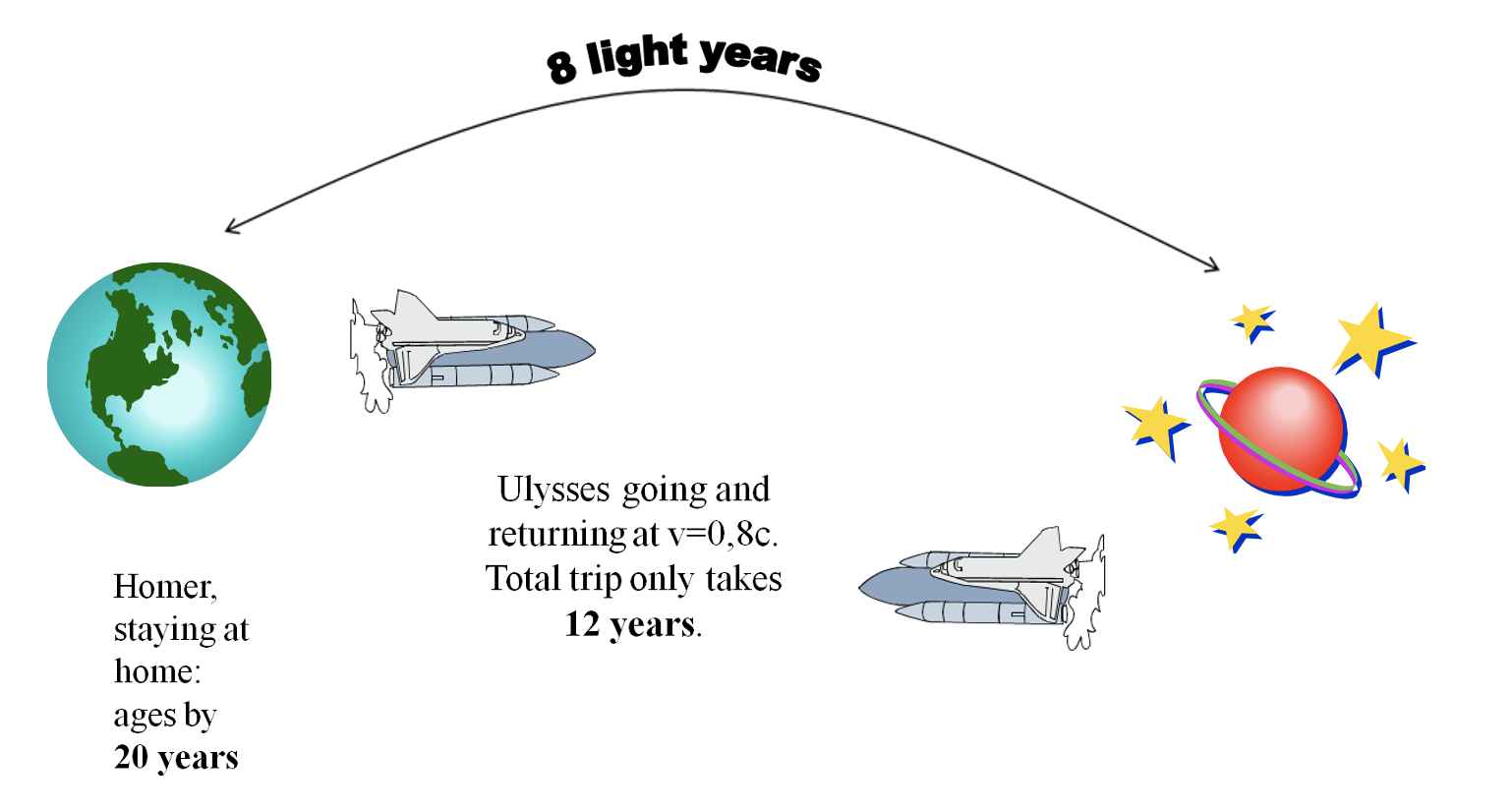
2.2 Traveling at high speeds, even if it is not the speed of light, c, has other unfamiliar and counterintuitive effects. Imagine an observer on Earth, clocking the duration of some event, E. If a fellow observer flies over the same event at high, very high speed, they will not measure the same duration for E. Clocks in fast-moving rockets slow down, as observed from Earth. This phenomenon is known as time dilation. It gives rise to what some regard as time travel into the future. To illustrate, consider an imaginary journey involving two twins: Homer and Ulysses. They decide to run an experiment. Homer will stay on Earth while Ulysses visits a distant planet, some 8 light years away. Ulysses’s spaceship travels at 80% of the speed of light (0.8c). Then according to Homer the journey there and back should take 20 years, 10 years for each leg. But not so for Ulysses. Ulysses’s clocks slow down, compared to Homer’s clocks. According to Ulysses’s clocks the round-trip will only take 12 years (fig. 4). As a consequence Ulysses will be younger than Homer on his return. It sounds paradoxical but it is “a consequence of time dilation, or the slowing down of the traveler’s clock relative to that of the twin.”[5]

During the trip, the twins will also be able to communicate with each other by exchanging signals, say once every year. From these signals they can calculate each other’s age. The signals will be Doppler-shifted, due to the speeds involved. The speeds will affect both the frequency, f, and the wavelength, λ, of the signals. (The speed of the wave is the product of the frequency of the wave multiplied by its wavelength.) Homer will receive 12 signals from Ulysses. He will be able to calculate that his brother will be 8 years younger when he returns to Earth. Ulysses will receive 20 signals from Homer. He will be able to infer from Homer’s signals that his brother will have aged 20 years. At one point the signals may stop. If Ulysses were able to travel close to the speed of light he would return to Earth in the distant future. In a way Ulysses would have travelled far into the future. A very fast moving time traveller would only age by 31.6 years in 500 years of Earth time. It is worth mentioning that the twin effect, that is the differential aging of the twins, is measurable, if not noticeable, in commercial pilots or frequent air travellers. They will age slightly less than their fellow citizens who remain on Earth. “So, to avoid aging, we should travel fast’, is Atkins’s advice.”[6]

Could Ulysses ever reach the speeds required for time travel into the distant future? Unfortunately, the closer a material object, like a spacecraft, gets to the speed of light, the ‘heavier’ it becomes. That is, its mass increases with speed. The mass would become infinite if it reached the speed of light. With the increase in mass, the energy needed to propel the spacecraft would also increase exponentially.

3. Nuclear Power.

The impossibility to accelerate objects to the speed of light follows from Einstein’s famous equation: E=mc². Einstein’s formula expresses the equivalence of mass and energy. A gain or loss of energy can equally be regarded as a gain or loss of mass. In the public’s mind this equation is associated with nuclear bombs. But it is very general and affects every object. For instance, an ordinary light bulb of 100W, which burns continuously for one year, will lose a tiny amount of mass (0.00000003kg). On the other end of the scale the sun loses about 4 billion kilograms of mass per second. As it is approximately 5 billion years old it will ‘only’ burn for another 5 billion years. If an object, say a tennis ball, could be completely converted into pure energy, it would generate enough electricity to power a whole city, like New York, for a certain amount of time.

Einstein’s famous relationship lies at the heart of nuclear power, which produces energy. It comes in two forms: nuclear fission and nuclear fusion. Both fission and fusion convert nuclear energy into thermal and electrical energy. In both cases energy is released because a bound system – the nucleus – has less mass than its constituent particles (protons and neutrons).  This so-called mass defect corresponds to the energy which is released when separate particles are joined to form an atomic nucleus.

The energy from nuclear reactions is far greater than the energy obtained from atomic or chemical processes. This is because the energy that holds the nuclei together – called binding energy – is far greater than the energy that keeps the electrons in their ‘orbit’ around the nucleus. In nuclear fission a heavy nucleus, like that of Uranium, splits into two light nuclei. In nuclear fusion two light nuclei combine to form a heavier nucleus. ‘The trick with fusion,” says John Gribbin, “is the opposite of the trick with fission.”[7] Nuclear fission does not normally occur naturally but the life cycle of stars, like the sun, is sustained by nuclear fusion. A typical reaction looks as follows: an incoming particle, x, collides with a nucleus, X, resulting in nucleus, Y, and particle, y. Q is the energy released in the reaction.

3.1 Fission was discovered, at the end of 1938, at the Kaiser Wilhelm Society for Chemistry (Berlin). It was the result of the cooperation of four scientists: Otto Hahn (1879-1968), Fritz Strassmann (1902-80), Lise Meitner (1878-1968) and Otto Frisch (1904-79). In the United States the first nuclear fission experiment was carried out at Columbia University in 1939.

Fission only occurs when nuclei contain more neutrons than protons. This process can be illustrated by the use of a model, the liquid-drop model. In this model a stable heavy nucleus is visualized as a liquid drop. A nucleus, like a uranium nucleus, ²³⁵U, (with 92 protons and 143 neutrons) can be disturbed when it absorbs a neutron. This leads to an excited nucleus, ²³⁶U (with 92 protons and 144 neutrons), which begins to vibrate and becomes unstable. The nucleus then splits apart, emitting several neutrons which can produce further fission. This leads to a chain reaction of fission events (fig. 5).

The fragments carry away a lot of the energy but this energy can be used to heat water. The resulting steam can then generate electricity in a turbine. The release of energy is uncontrolled in a nuclear weapon but carefully controlled in a nuclear reactor.

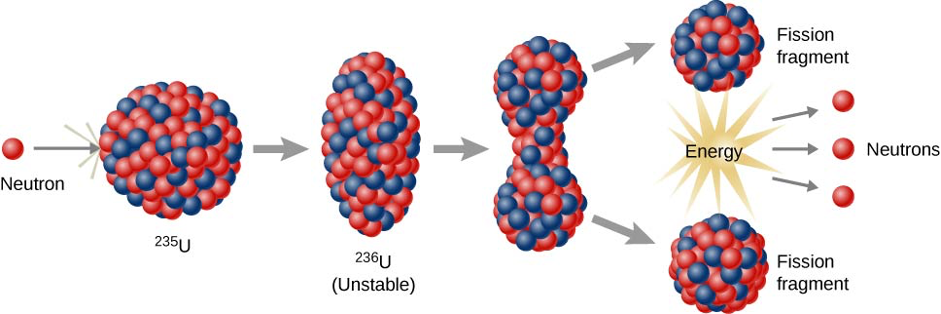
Note regarding fig. 5: Typical fission events release 200 mega-electron volts (200Mev) of energy (=8.9×10^-18kWh). 1 mega-electron volt is one million electron volts. Watt is a unit of power – energy per unit time. It specifies the rate at which electromagnetic energy is absorbed or radiated. The average household uses approximately 1,350 kWh per month.

As most people are aware one of the biggest problems with nuclear fission is nuclear waste. It remains radioactive for many centuries and poses a threat to the biological and social environment.

3.2 Scientists and engineers have therefore tried for decades to obtain energy from nuclear fusion (fig. 6). In nuclear fusion two light nuclei, for instance deuterium (²H, also known as heavy hydrogen) and tritium (³H) collide to fuse into a heavier nucleus, helium ⁴He and a neutron, n. Such processes can be tested in laboratories. They are important because fusion produces three to four times more energy than fission.  The energy released, Q, is the excess energy that is no longer needed to bind the heavy nucleus together; the corresponding decrease of mass is converted into energy in accordance with Einstein’s equation. In Figure 6, Q = 14.1 MeV + 3.5 MeV (= 17.6MeV). In concrete terms, if 2 kilograms of deuterium were mixed with 3 kilograms of tritium, 20 grams of mass would be converted into other forms of energy, enough to heat 50,000 homes for a year.

A major difficulty in producing energy from nuclear fusion is that it requires extreme pressures or temperatures. Such excessive temperatures, for instance of the order of 10⁸ Kelvin (which corresponds to 180 million °Fahrenheit or 100 million° Celsius), are needed to overcome the repulsive force between the two nuclei. Scientific progress has been slow but European scientists, at the JET laboratory in the UK, have recently reported a major breakthrough in their quest to develop practical nuclear fusion (February 2022). By squeezing together two forms of hydrogen, the experiment produced 59 megajoules of energy over 11 seconds. This corresponds to 11 megawatt of power, enough to boil approximately 60 kettles of water.  The BBC’s Jonathan Amos quoted the head of operations at the reactor lab, Dr. Joe Milnes, as saying that the “JET experiments put us a step closer to nuclear fusion.”[8] The British astronomer Arthur Eddington (1882-1944) proposed in 1920 that stellar energy could result from hydrogen-helium fusion. In our solar system it is only the sun which reaches temperatures of 150 million °C (or 27 million °F) at its core. Very schematically, the sun converts hydrogen nuclei into helium nuclei. Each fusion reaction liberates about 26.7 MeV of energy. The total energy output of the sun is about 4×10²⁶W, of which the Earth receives about 1.4×10³Watts per square meter (m²).

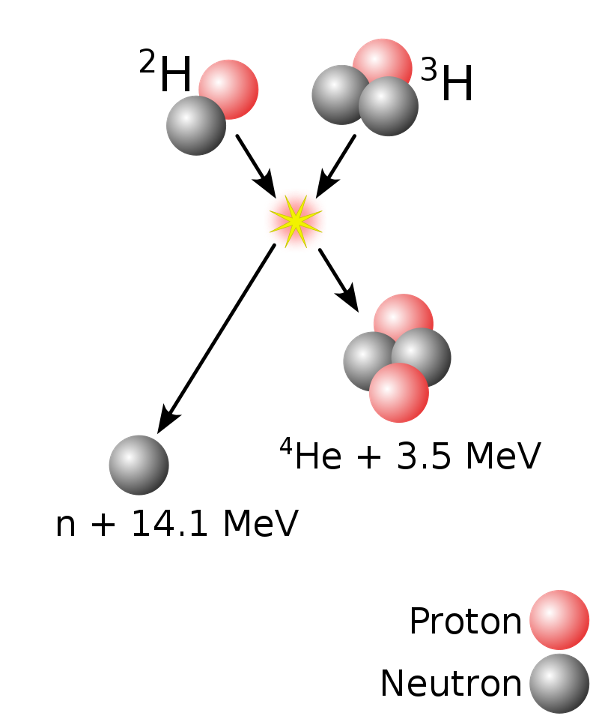
Here deuterium (1 proton and 1 neutron) is fused with tritium (1 proton and 2 neutrons) to result in helium (2 protons and 2 neutrons) plus 1 extra neutron. The resulting energy is 17.6 MeV = 7.83×10^-19 kWh.

4. Technological Applications of the General Theory.

Let us go back to the strange behaviour of clocks according to the Theory of Relativity. Clocks, which move very fast, appear to slow down according to observers who are at rest with respect to the moving clock. The travelling twin, Ullyses, returns to Earth younger than his twin brother. This scenario, however, neglects gravity. It was Einstein’s stroke of pure genius to realize, as Carlo Rovelli puts it, that “the gravitational field is not diffused through space; the gravitational field is that space itself. This is the idea of the theory of general relativity. Newton’s “space”, through which things move, and the ‘gravitational field’ are one and the same thing.”[9] What happens to clocks in gravitational fields? The short answer is: when gravitation is weak, for instance high above the Earth, clocks run faster. A clock on top of a tower runs measurably faster than a clock at the bottom.

Earlier it was stated that pilots, after a long career, will be younger than their fellow citizens who fly only rarely. The General Theory adds a complicating factor. Clocks at altitude run faster than clocks closer to the surface of the Earth. So if the task were to calculate how much younger a pilot will be, the effect of motions (clocks slow down) and of gravity (clocks at altitude run faster than clocks on the ground) have to be taken into account. These effects are not noticeable on the human scale but they can be measured by very precise atomic clocks. They are important for understanding how GPS (Global Positioning System) works. That is, time is important for navigation. And as very fast signals are involved the Theory of Relativity has to be taken into account.

4.1 GPS was an invention of the US military. It used to be called ‘Navstar’ and the first satellite was launched in 1978. The system was fully functional by 1995. It was first used in cars in 1996 and was made available for free civilian use in May 2000. Today GPS forms part of every iPhone and has become an indispensable tool for most of us. It is a brilliant piece of technology but it would not be possible without the application of the General Theory of Relativity. This theory is essential for the study of cosmological phenomena, such as black holes or the expansion of the universe. Its application in the running of clocks is indispensable for the functioning of GPS.

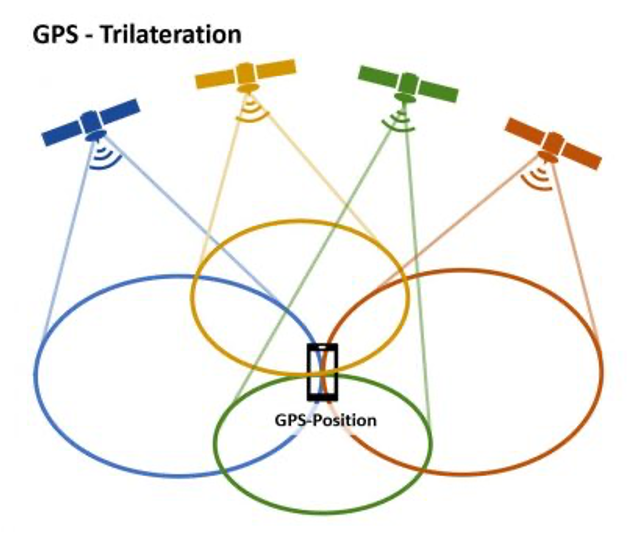
So how does GPS work? As all users know, GPS locates their position almost everywhere on Earth. An iPhone does not need an internet connection but it must be able to receive radio signals from satellites orbiting the Earth. GPS requires a system of satellites, which continuously orbit the Earth, sending radio signals at regular intervals. They measure the distance between the satellite and the location on Earth.  Altogether there are 32 satellites, 24 of which are core satellites and 8 are emergency replacements in case something goes wrong. They have a lifetime of approximately 10 years and orbit the Earth at an altitude of about 20,000 kilometres. In order to locate a position on Earth four satellites are needed. They use a technique called ‘trilateration’ which means that the coordinates of these satellites are coordinated in such a way that they can pinpoint a location on Earth.

To visualize the pinpointing, imagine that the satellites project circles onto the surface of the Earth (fig. 7). The GPS receiver will be located where these circles intersect. The more circles are drawn, the more precise the location will be. Imagine that you find yourself in a place without really knowing your whereabouts. You ask people around you. But instead of telling you that you are in Ann Arbor, Michigan, they tell you how far you are from nearby places. One person informs you that you are 43 miles from Detroit. That information is not useful to you because there are many places, which fit this description. Another person says that you are 241 miles from Chicago. If you draw large circles around Detroit and Chicago they will intersect. But the area of intersection is too large to identify your position. You need to draw further circles. So another person specifies that you are 65 miles from Lansing. Again you draw a circle with Lansing as its centre. You see: the more circles you draw the more precise the location will become. It narrows down the intersection area of the circles. And this is what happens in GPS. Except that now it is not circles that are drawn on a map but imaginary spheres around a satellite. Your location is where these spheres intersect (fig. 8).

One important element of this explanation is still missing and it involves time. The satellites are equipped with very precise atomic clocks, which are controlled and updated from over 50 ground-based stations. But the receiver – the mobile phone – only has a quartz clock. The satellites send intermittent radio signals down to Earth, at time t₁. The signals travel at the speed of light, c. They contain the exact time and location of the satellites. A mobile phone receives the signals at a slighter later time, t₂.

The distance between the satellite and the mobile phone is the interval between the time of emission, t₁, and the time of reception, t₂, multiplied by the speed of light, c.

The problem is that the receiver clock is not as precise as the atomic clock. A temporal difference exists between the atomic clock and the receiver clock. This drift is called a ‘time offset’, in symbols: Δt_offset. This time offset is the same for every satellite because their atomic clocks are perfectly synchronized.

The inaccuracy of the receiver clocks, compared with the atomic clocks, means that these clocks are not perfectly synchronized. The atomic clock and the receiver clock do not agree when the signal arrives at the mobile phone. It can cause serious errors in GPS calculations. An error of a few microseconds can result in errors of several kilometres due to the speed of light. As there is a time offset between the atomic clock and the receiver clock, Δt_offset, the interval between satellite and mobile phone is no longer simply t₂ minus t₁ (x velocity) but t₂ ± Δt_offset. A fourth satellite is needed to solve the unknown time offset and to improve the accuracy of the position. To summarize: three satellites determine the longitude, latitude and altitude of the satellite and a fourth satellite solves the temporal discrepancy between atomic and quartz clock (fig. 9).

This situation is comparable to ordinary experience. If you arrange to meet a friend at a certain time at a specific location but your respective watches do not agree, you will miss each other. In order to prevent this from happening, your watches should be synchronized by reference to a master clock.

The determination of time has to take two factors into account. As the satellites move very fast their clocks slow down compared with clocks on Earth. This slowing down of clocks due to their motion is the well-known time dilation effect of the Special Theory, which was mentioned above in connection with the twin effect. But now an additional factor comes into play. The satellites orbit the Earth at 20,000 kilometres where the gravitational effect of the Earth is weaker. Clocks in weak gravitational fields run faster than their counterparts on Earth. These effects have to be added up: atomic clocks run slower by 7 microseconds per day due to their motion; and they run faster by 45 microseconds due to their altitude. (A microsecond is one millionth of a second.) This makes a difference of 38 microseconds a day. The rate of atomic clocks must be adjusted. Without such corrections GPS would produce errors of around 10 kilometres per 24 hours.

5. Conclusion.

The technological applications of the Theory of Relativity thanks to the Doppler Effect, the equivalence of mass and energy, and the behaviour of clocks illustrate the tight connection between science and technology. Sometimes technology proceeds in the absence of theoretical science. Ancient water clocks and sun dials could be built without correct astronomical knowledge. A clever craftsman may build a house or a bridge without scientific knowledge. The great Dutch scientist, Christiaan Huygens (1629-1695), needed physics to build the first pendulum clock (1656). In 1676 the Danish physicist Olaf Rømer (1644-1710) determined the velocity of light by observations of the Jupiter moons; he found the value of c ≈ 225,000 kilometres per second (or 2.25×10⁸m/s, which is relatively close to the modern value of 2.99×10⁸ metres per second in vacuum). The more sophisticated the technology, the more scientific knowledge is required.  The technology discussed in this article is firmly based on the theory of relativity. Quantum theory – the theory of atoms and subatomic particles – also leads to unimaginable technological spin-offs.

Still GPS is not fool-proof. A Swiss milkman ended up on a mountain, from which he had to be rescued; some tourists drove a rental car into a lake at night. Even with GPS common-sense is advisable.

Endnotes

*As noted in the Introduction, Digital pieces with *Guest Author in the title have been through the following process:

• Content editing by executive editor or ad hoc editor
• Peer Review with one reviewer
• Copyediting by executive editor