Friedel Weinert
Technological Applications of Quantum Mechanics
The great American physicist Richard Feynman (1918-1988) once claimed that nobody understood Quantum Mechanics (QM). He did not mean the mathematics but the strange and weird phenomena, which are associated with the theory. These bizarre phenomena cannot be explained by reliance on classical physics. If one tries to explain the behaviour of atomic and subatomic particles by reference to classical mechanics, one gets the wrong answers. That is, the answers do not correspond to the measurable and observable behaviour of quantum particles. “The world of an atom looks nothing like what we think of when we visualize matter” writes Harvard physicist Lisa Randall.[1] Hence physicists were forced to develop a new kind of physics: Quantum Theory or the physics of atomic behaviour. (Atoms are systems, which consists of a nucleus – plural: nuclei – surrounded by electron clouds. The nuclei themselves are made up of positively charged protons and neutral neutrons.) This new theory was developed over several decades, from 1912 to 1925. It is now one of the most successful scientific theories that have ever been invented. As with the General Theory of Relativity the mathematics is complicated but the phenomena can be readily understood. Until the early 1990s Quantum Mechanics was seen as an arcane scientific activity. Then, suddenly, the prospect of technological applications emerged. This article will focus on two applications of QM: lasers and Quantum Information (i.e. quantum cryptography, teleportation, and quantum computation). The working of lasers can be explained by considering the manipulations of photons, i.e. massless particles of light. Quantum Information requires a consideration of unfamiliar states of quantum particles, best described as entanglement and superposition.
- Lasers.
A laser is essentially an optical amplifier. The term laser is an acronym that stands for light amplification by the stimulated emission of radiation. The key terms are amplification and stimulated emission. The technological development of lasers began in the 1950s, but Albert Einstein (1917) laid the theoretical foundations.
Einstein wished to understand how matter interacted with electromagnetic radiation. He distinguished three processes:
- stimulated (or induced) absorption occurs when an atom absorbs a photon;
- spontaneous emission occurs when an atom in an excited state emits a photon of a certain amount of energy;
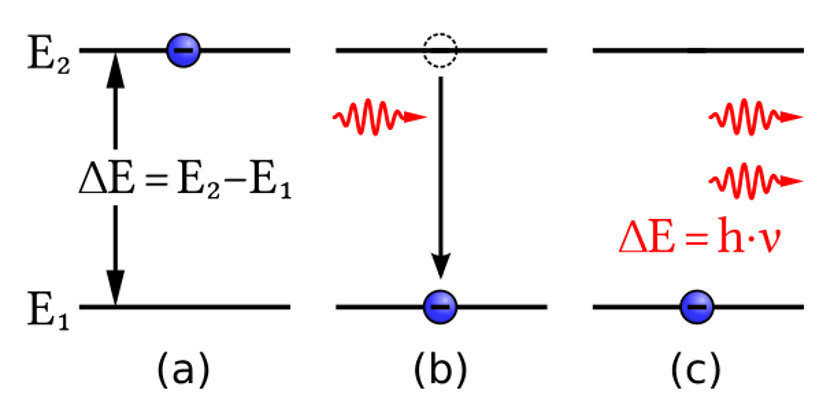
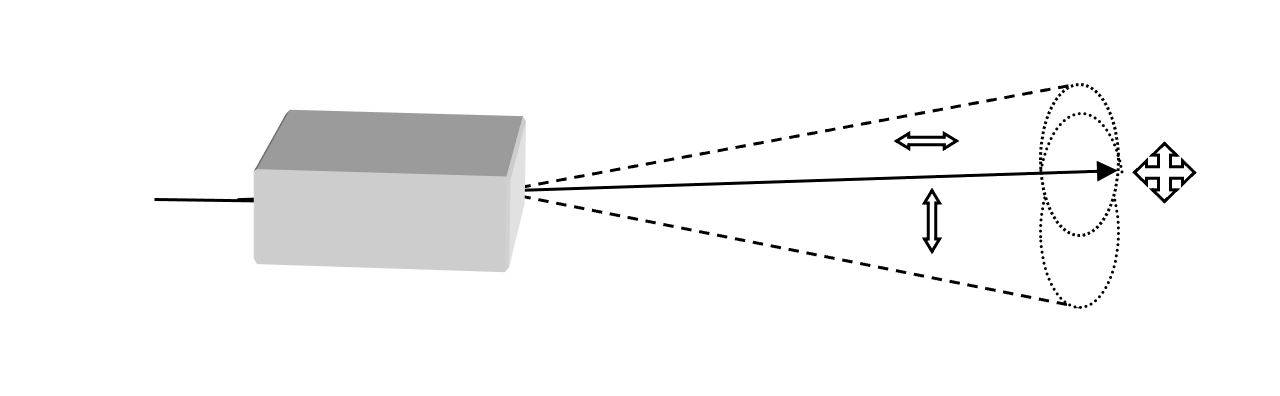
- the last process, stimulated (or induced) emission, is central for the workings of a laser (fig. 1a).
Stimulated emission was a previously undiscovered form of radiation. In this process an atom is in an excited state. A passing photon (of the right energy) induces the atom to emit a photon and to make a transition to a lower energy state. Two photons emerge (fig. 1b). They can interact with other excited atoms in the system, inducing more excited atoms to release photons. They are all in phase with each other. The process cascades leading to light amplification by stimulated emission of radiation.
The important point is that the two emerging photons are travelling in exactly the same direction with exactly the same energy (or frequency) and the same intensity. That is, all photons share the same quantum-mechanical state: a laser is a truly coherent light source. “Laser light is coherent light, in which all the light waves are in phase; hence the power of lasers.”[2] As coherent laser light is very focussed it can be narrowed to a tiny diameter. These characteristics make it possible to drill minute holes and make tiny cuts in hard, dense material. (Real light sources, say from a torch or a star, emit light via the uncorrelated action of many atoms, involving many different wavelengths.)

What has been presented is a simplified process. To make it more realistic, consider a collection of atoms, all in the same excited state, and again an incident photon causing induced emission of two photons. Each of these two photons causes induced emission processes in turn, resulting in more photons. Eventually an intense beam of photons will result, all coherent and moving in the same direction. This is the basis of the operation of a laser. Unfortunately, there are several problems, which would prevent this simple model from working. First, it is very difficult to keep a collection of atoms in the required excited state; the danger is that some atoms will emit photons spontaneously. The second reason is that atoms that happen to be in their ground state will spontaneously absorb photons from the beam as it builds up. These difficulties can be solved by a four-level laser, as for instance the helium-neon laser (fig. 2).
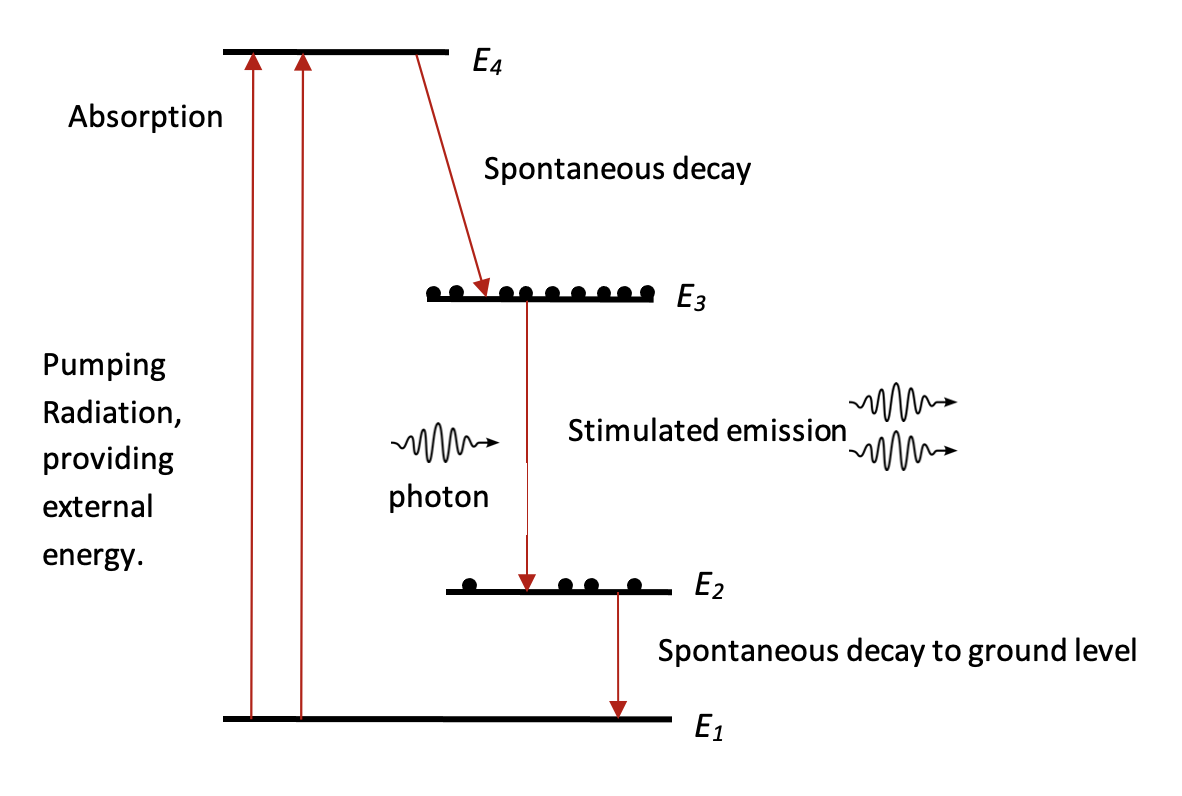
In such a four-level laser atom the ground state, E1, is pumped to an excited state, E4, that decays rapidly to metastable state, E3. It is called a metastable state because it has a long lifetime, typically 10-3 seconds, whereas most excited levels in atoms may decay in 10-8 seconds.
Yet one essential element is still missing. In order for stimulated emission to work, there must be more photons in the higher state than in the lower state. This amplification process is called population inversion and is obtained by providing an external source of energy. This method is called optical pumping. It is essentially the intense irradiation of the laser with auxiliary radiation in order to excite as many atoms as possible into a higher energy state, that is from state E1 to state E4. Stimulated emission occurs when the atoms transit to another excited state, E2. The level E2 is short-lived and rapidly decays to the ground state E1. This is still a simplified presentation: amplification can also take place by microwaves (in which case it is called a maser), and the energy levels of atoms are more complicated than indicated. In fact, many different methods can now be employed to get a collection of atoms in the same excited states. The photons they produce lead to different laser lights.
As is well known lasers are used in numerous applications: they serve as surgical tools in medicine, in check-out scanners, laser guns and laser printers. The basics of lasers can be understood without talk of the uncanny behaviour of subatomic particles, which are essential for other applications, i.e. the broad area of Quantum Information. These eerie phenomena are known as superposition and entanglement.
2. Quantum Information.
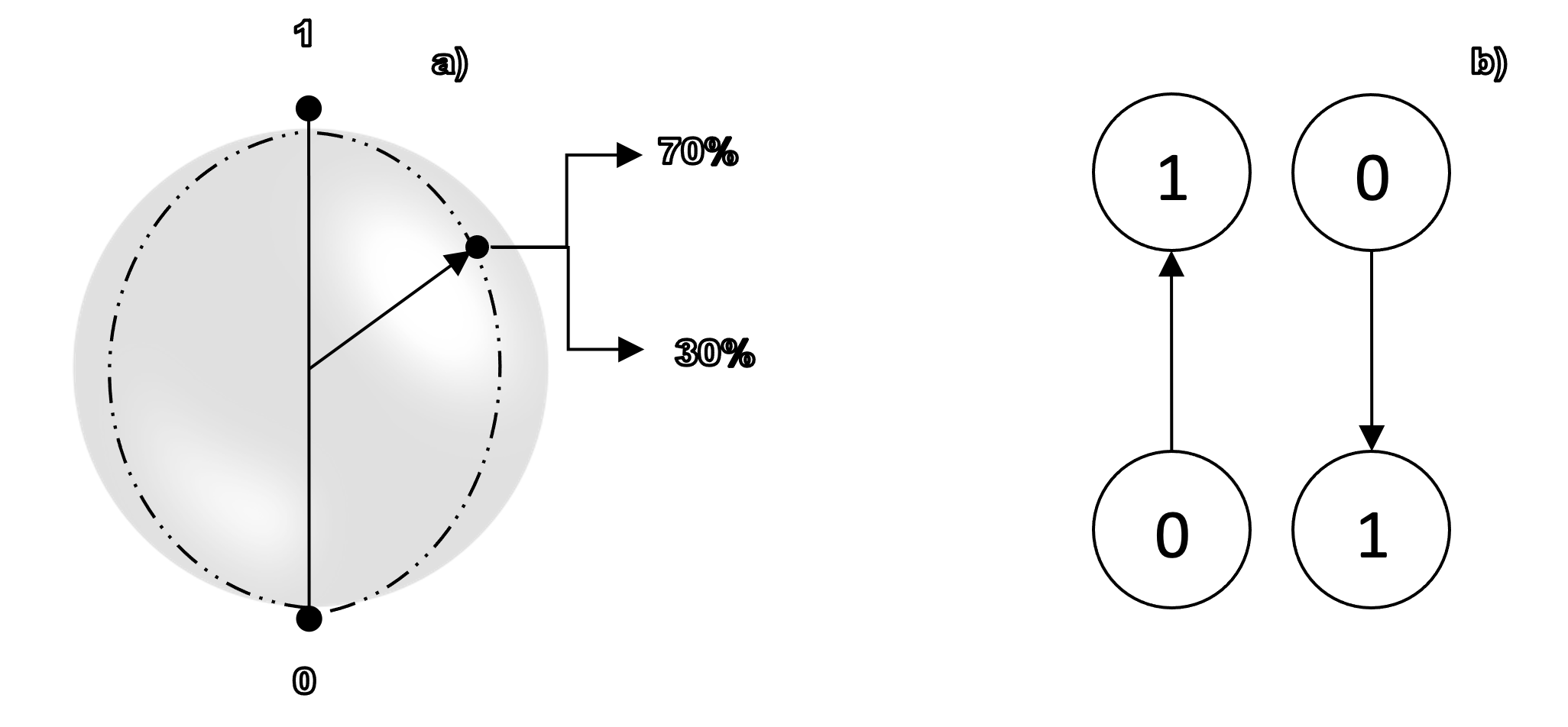
Quantum Information encompasses quantum cryptography, teleportation, and quantum computation. It treats information as a physical resource. As Anton Zeilinger points out the “important new observation is that information is not independent of the physical laws used to store and process it.”[3] The classical unit of information is the bit, which can exist in one of two states: 0 or 1 (‘yes’ or ‘no’, ‘true’ or ‘false’; ‘on’ or ‘off’). It can be represented by a transistor switch as ‘off’ or ‘on’, by magnetic regions on a disk or pencil mark on a piece of paper. The science of quantum information generalizes this classical source of information to quantum bits or qubits. Just like bits, qubits can be represented by different physical means: for instance energy levels of atoms, the spin of a particle, like an electron, or the polarization of a light photon. Both bits and qubits are described by their states, 1 or 0 and |0> and |1>, respectively.
2. 1. The quantum world reveals striking, new phenomena. In Quantum Mechanics any object that is in two different quantum states, say spin or polarization, also has a range of other possible states, called superpositions. Superpositions occur when two separate quantum states are added together, resulting in a new state. A quantum bit can exist in both states, |0> and |1>, simultaneously. An electron, for instance, can travel through two slits (one upper, one lower) at the same time. “The weirdness of quantum mechanics really kicks in when a particle is superposed with itself.”[4] It may help to visualize qubit states as arrows pointing to a location on the surface of a sphere: let ‘1’ represent the North Pole and ‘0’ the South Pole. Between the North and South Poles there are many other states, as shown by an arrow pointing to a location between North and South (fig. 3a). In other words, quantum states can be added together or ‘superposed’, such that every quantum state can be represented as the sum of two or more other distinct states. As qubits can be in a superposition of |0> and |1>, they can store |0> and |1> simultaneously. A particularly important method is the use of the polarization states of photons. Light consists of electromagnetic oscillations. It is usually unpolarized. That is, it vibrates in all directions, perpendicular to the photon’s path. But it can be polarized, as in sun glasses. This means that only certain oscillations are let through: for instance, horizontal, vertical or diagonal. If, say, a photon has a vertical or horizontal polarization, |0> and |1>, it can also be in a superposition of horizontal (↔) and vertical polarization (↕︎), that is in the superposed state (⤧). The same is true of the diagonal directions. However, when these states are measured, only one will be detected.
The Austrian physicist Erwin Schrödinger (1887-1961) used a striking illustration of superposition. It involved a cat in a sealed box with a radioactive atom. This thought experiment is known as Schrödinger’s Cat. The atom exists in a superposition of ‘decayed’ and ‘not decayed’. This corresponds to a cat state that hovers in a superposition of being both alive and dead. But when the box is opened the cat is found either dead or alive, depending on whether the atom has decayed or not. Before the measurement a strange ‘both-and’ logic applies; after the measurement it is the familiar ‘either-or’ logic.
2. 2. The superposition of the states of a single system, like an electron, is an important feature of Quantum Mechanics. But for the purpose of explaining quantum information another important feature emerges. It occurs when groups of two or more quantum objects or qubits are joined. Such systems can exist in entangled states (figs. 4a, b). “Entanglement describes correlations between quantum systems that are much stronger than any classical correlations.”[5]
Entangled particles constitute a composite system, that is, a system that consists of two or more subsystems. When quantum systems are entangled they lose their own individual quantum properties; only the whole system has a well-defined state. Entangled electrons and photons behave like a single entity. Surprisingly, their entangled states do not depend on distance. A measurement of one of the pairs immediately provides information about the state of the other component. Imagine that two ordinary coins could be ‘entangled’ as if they were quantum particles. They could exist in a superposition of heads and tails. Entanglement means that if one coin were measured as head up, the other would immediately show as tail up, or vice versa. If two photons are entangled, then a measurement on the polarization of one photon, say vertical, immediately shows the other photon in the opposite polarization state, horizontal, even though they may be miles apart. In the language of qubits: If one measures |0> , the other shows |1>, or vice versa. Entanglement is the key feature of many applications of Quantum Mechanics. Not only is it a physical source, like energy, it comes in degrees. That is, the more entanglement is available the more quantum information processing can take place. Erwin Schrödinger regarded entanglement as the most characteristic feature of Quantum Mechanics. Entanglement leads to mysterious correlations between widely separated quantum objects. Einstein called it “spooky action at a distance.”[6]
3. Quantum Cryptography.
In modern communication systems the central questions are: How to send messages that cannot be read by unintended recipients? How to make conference calls and financial transactions secure? How to thwart cyber attacks? “Cryptography is the art of hiding information in a string of bits that are meaningless to any unauthorized party.”[7] Traditionally one way of achieving security lay in the art of encrypting messages. For instance, a simple greeting like ‘hello’ can be encrypted by replacing the letters by their numerical place in the alphabet: 85121215, since ‘h’ is the eighth letter in the alphabet and ‘o’ is the fifteenth letter etc. In order for this to work the recipient has to receive a key, which allows that person to decrypt the message. The weak point of this system is that the sender and the recipient must agree on and share the key. An even weaker point is that neither the sender nor the recipient of the message can ever know for sure whether or not the message has been intercepted. Once a third party knows the key they will be able to read all messages that are exchanged between sender and recipient.
In order to overcome these weaknesses Quantum Cryptography offers several advantages. It employs the weird nature of Quantum Mechanics. It allows two physically separated parties, say Alice and Bob, to create a random secret key without the need to exchange it; the key can be used to encrypt and decrypt messages. Quantum Cryptography also allows the two parties to detect and evade eventual eavesdroppers. The technique enables them to verify that the key has not been intercepted. But Quantum Cryptography can achieve more: by encrypting sensitive data commercial companies all over the world can thwart cyber attacks. Hackers will no longer be able to read encrypted data and extract millions of dollars.
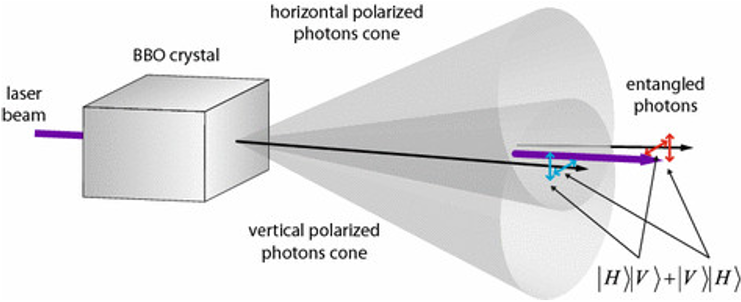
At present Quantum Cryptography employs two different protocols or techniques. Both use quantum states of photons – their polarization – to create a secret key and transmit secure information. The BB84 protocol uses single photons to create an encryption key; the other, newer technique uses entangled photons (see fig. 4a).
Let us briefly discuss how they work.
3. 1. The use of entangled photons was the brain child of the physicist Artur Eckert, based at Oxford University (1991). The idea was first implemented by a group at Innsbruck University under the leadership of Anton Zeilinger. Their experiments continued when Zeilinger’s group moved to Vienna. First, a pair of entangled photons is created. Alice receives one and Bob receives the other. Recall that entanglement means that the entangled photons lose their individual properties. The individual photons are unpolarized but the polarization state of the pair is entangled. When one of the photons is measured, it adopts one of two polarization directions: either horizontal or vertical. The other photon, no matter how far away it is, immediately adopts the opposite direction. This is one of the mysterious features of Quantum Mechanics: Einstein’s ‘spooky-action-at-a-distance’ is entanglement in action.
Imagine that Alice measures the following sequences of polarized photons:
HVVHVHHHVHV
(where H stands for horizontal polarization and V stands for vertical polarization). Bob immediately receives the opposite (orthogonal) polarization:
VHHVHVVVHVH.
Next Alice and Bob translate the random sequence into numbers, that is a series of 0s (for horizontal) and 1s (for vertical). Alice’s sequence then becomes
01101000101.
Bob does the opposite. He turns every V into a 0 and every H into a 1. His sequence becomes
01101000101.
This randomly produced sequence of numbers is the key they use to encrypt and decrypt their message. For the sake of simplicity it has been assumed that the photon pair only has two orientations. In reality it can also assume two diagonal polarizations (see fig. 5). Quantum Cryptography has two advantages over traditional methods: a) the results are random, since Alice has no control over them; b) the secret key does not have to be transferred to Bob since it is created simultaneously. Alice’s measurement produces a polarized state, whereupon the other photon adopts the opposite polarization.
An eavesdropper can, of course, intercept the transmitted photons. But eavesdropping can be thwarted in various ways. First, there is the random nature of the orientation. The eavesdropper must guess which orientations Alice has obtained. Second, when the photons do not match up, it will be obvious to the sender and receiver that something is wrong. In order to make life even more difficult for code breakers, a new key can be generated with every new message. Finally, Alice and Bob are also free to change the orientation of the polarizers for every interaction.
3. 2. The second method is the BB84 protocol, which was proposed by the American Charles Bennett and the Canadian Jules Brassard. According to this method unpolarized photons enter filters, which lead to either a horizontal/vertical or a diagonal direction ±45° (fig. 5). The process breaks down into several steps.
A. The sender (Alice) has a light source and four filters (green, yellow, purple and blue in fig. 5). For each photon she sends down an optical fibre, she chooses one of these filters at random. This results in a string of randomly polarized photons, which she records. There are four possible polarization states and bit designations: Vertical (blue: One bit), Horizontal (purple: Zero bit), 45 degree right (yellow: One bit), or 45 degree left (green: Zero bit). (Row 1: Alice’s bit sequence).
B. The photons travel to a receiver (Bob), who uses two beam splitters (horizontal/vertical and diagonal: ±45°) to “read” the polarization of each photon. When he expects a photon to arrive he chooses a detector basis at random: horizontal/vertical or diagonal: ±45°. (Row 2: Bob’s detection basis). If Bob chooses an analyzer that is incompatible with Alice’s choice of polarization, he will not be able to obtain any information about the state of the photon.
C. Once the stream of photons has been sent, Bob tells Alice whether or not he detected a signal, which beam splitter he used for each of the photons in the sequence they were sent (row 3). But he does not tell her which results he recorded.
D. Alice compares that information with the sequence of polarizers she used to send the key. She tells Bob when his analyzer is compatible with the polarization of the photon she sent. That is, Alice tells Bob which ones he chose correctly. If Bob uses the wrong beam splitter to read the photons the bits are discarded. The remaining sequence of bits becomes the encryption key (row 4). Alice and Bob can now be sure that they have the same values and can be used to generate a secret key.
Once they have the key Alice can encrypt messages, which Bob can decrypt. The message will be secure because the polarization is chosen at random and the key is created simultaneously. The method is safe because an eavesdropper would have to guess the polarization. As it is random the eavesdropper would get it wrong in 75% of the bit values. Alice and Bob would notice that photons with the wrong polarization have been sent. If this happens too many times, they will be alerted that the key is no longer secure.
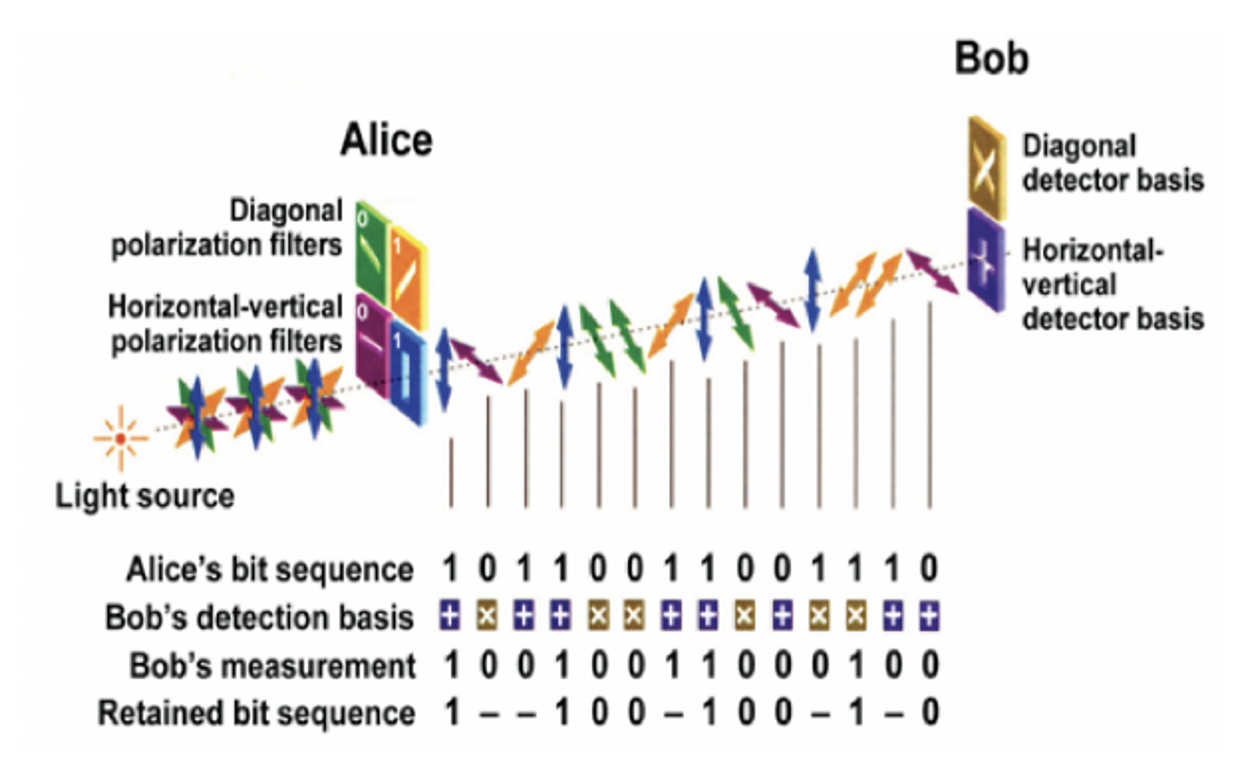
When the analyzers used to polarize the photons are compatible with the polarizers used to ‘read’ the photon, the bit is retained. Whenever this is not the case, the bit is discarded. The secret key is used only when Alice and Bob agree about the outcome and the same filters were used.
Consider some of the columns to see what is going on.
Column 1: Alice sends a vertically polarized photon (blue: 1). Bob chooses a horizontal/vertical analyzer to read correctly the polarization of this photon (1). As Bob’s analyzer is compatible with the polarization of the photon, which Alice sent, this bit is retained.
Column 2: Alice sends a horizontally polarized photon (purple: 0) but Bob uses a diagonal detector to read the photon’s polarization. Although he measures (0), he uses the wrong analyzer so this bit is discarded.
Column 3: Alice sends a diagonally polarized photon (45° right, yellow: 1) but Bob, using a horizontal/vertical detector, measures a horizontal polarization.
Column 4: Alice sends and Bob detects a vertically polarized photon (blue: 1).
(…) Column 9: Alice sends a diagonally polarized photon (45° left, green: 0), which Bob detects with the right analyzer.
4. Teleportation
Another area of Quantum Information covers the ‘teleporting’ of information. In science fiction large objects, including people, are teleported (‘beamed’) from one station to a far-flung place. The original object is scanned; the extracted information is sent to a distant receiving station, where the information is used to create an exact replica of the original. Unfortunately, Quantum Mechanics forbids the teleportation of large objects because no perfect scan of such objects can be made. That is, the precise location and momentum of every particle in the object cannot be known at the same time. (This is the gist of Heisenberg’s uncertainty principle. It means, as Randall explains “that the accuracy with which position is known limits the maximum precision with which one can measure momentum.”)[8]
Therefore, a method has to be found, which allows the transmission of information, from A to B, without measuring it. Quantum Mechanics makes this possible via entanglement. As photons can be entangled, they can be teleported. In the teleportation of photons between two stations, it is not the particles which travel. Rather they are replicated; i.e. one signal is dismantled and replicated in the sister station. The reason for using entangled particles is that, according to a fundamental principle (No cloning theorem) a quantum particle can never be cloned. So Alice cannot just send a copy of her photon to Bob. But it is possible to transfer the quantum state of a particle to another particle as long as no information is obtained about the state.
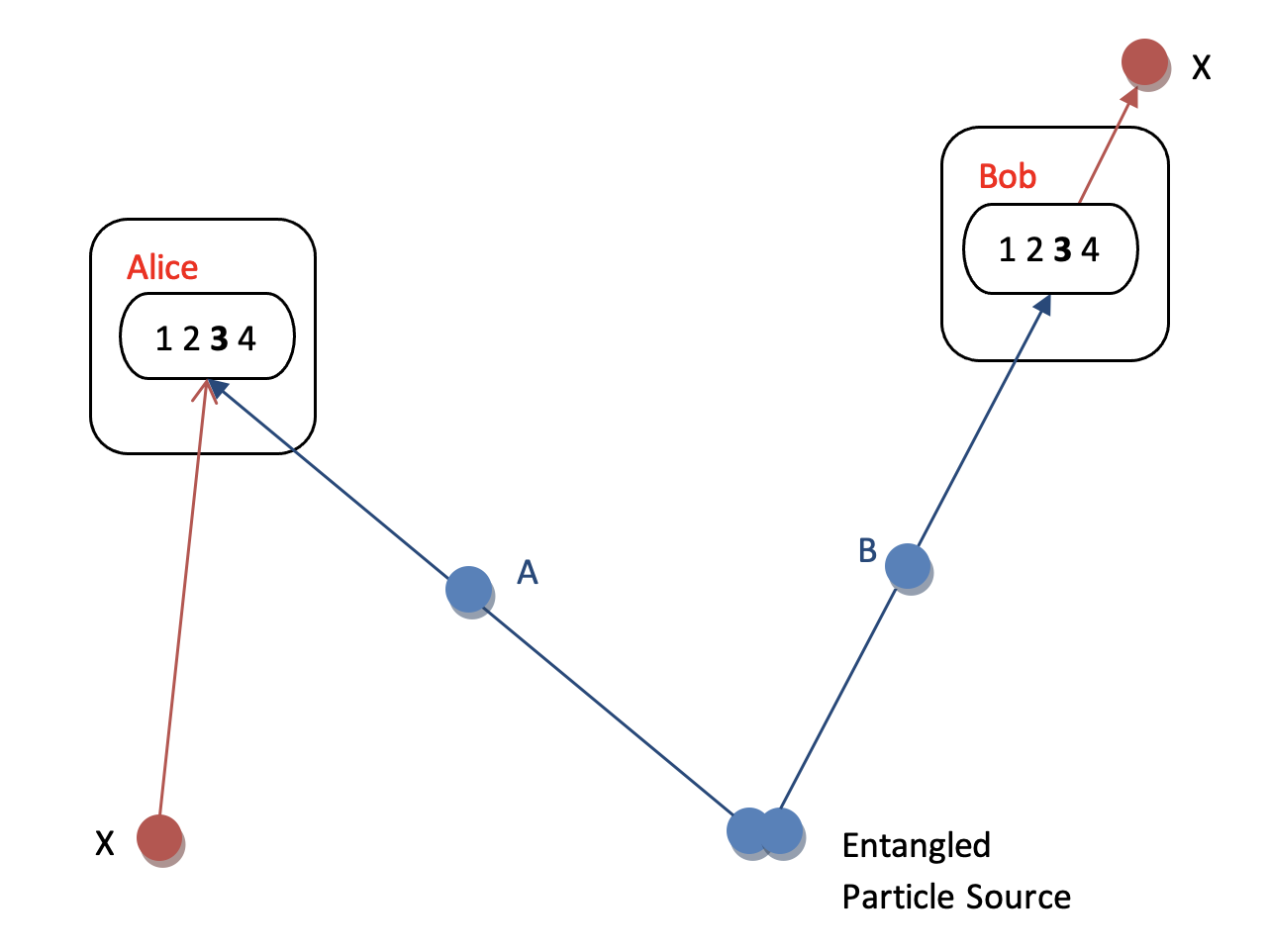
How are photons teleported? Imagine that Alice has a quantum system in an unknown state and wants Bob to have exactly the same system. She needs an entangled pair of photons (A & B) and a third photon, X. Alice gets photon A and Bob photon B. Alice wants to send X to Bob. She does not know the state of X but she wants Bob to have the same polarization state as X. To teleport photon X Alice measures A and X jointly but, due to the entangled state, she does not know which polarization each photon has individually. Her results are random, since there are four possibilities, i.e. four polarization states, corresponding to four quantum relations between Alice’s photon A and photon X.
To complete the teleportation Alice must send a message to Bob, via conventional means, which informs Bob about the result of her measurement. After receiving the message Bob can transform his photon B, if necessary, so that it becomes an exact replica of photon X. Bob, for instance, may shift his polarization by 90°. Photon X now appears in a different place with all the features of the ‘original’, which has disappeared from Alice’s station (fig. 6)
What is the use of all this? In the future teleportation could be used to transfer financial information between commercial and governmental agencies. Although the teleportation of photons is still at an experimental stage, it has been achieved in several experiments. Anton Zeilinger’s group teleported information over several hundreds meters. Not far away in Geneva, Nicholas Gisin and his colleagues achieved teleportation over a total of sixteen kilometres.[9]
5. Quantum Computation
Computers work on information, which can be represented in bits and qubits. Quantum computation provides new opportunities because qubits can exist in superpositions and entanglements of |0> and |1>. As two pioneers in the field put it: “Quantum computation is all about making the invisible aspects of the particle – its counterparts in other universes – work for us.”[10] The superpositions of the qubits do not have to be of equal size, just as an arrow on a sphere can point more to the south than the north. Such superpositions cannot be realized in traditional computers, because they operate according to principles of classical physics. Furthermore quantum computers can process two bits of information by using just one photon. Quantum computers are at present far from realization. But their potential is limitless. Quantum systems can make computers faster and they can support entirely new modes of computation.
A quantum computer can work on a large number of inputs simultaneously and it can do so much faster than conventional computers. This is because more than two qubits – such as energy levels in an atom, photons or spins of atomic nuclei – can be entangled and because they can exist in arbitrary proportions, as indicated in Figure 3a. Superpositions enormously increase the storage capacity of a register, typically a recording device.
A classical register, consisting of 3 bits, can be in one of eight different configurations: 000, 001, 010…,111. But a quantum register consisting of three qubits can store up to eight numbers at the same time. The more qubits are added the more quantum information can be stored. A register made up of 250 atoms (a 250-qubit register) could hold more numbers than there are atoms in the universe. A quantum computer can perform the same mathematical operation on a given number of inputs in a single computational step. This is because a quantum computer can compute a superposition of states at the same time: this form of parallelism means that a quantum computer can perform traditional computing tasks, like factorizing large numbers, much faster than standard computers. A quantum computer would find the prime factors of a very large number (say, 300 digits: 14728…..3) in less than a second, whereas a standard computer would take 150,000 years. Chess-playing quantum computers can analyze a trillion possible moves from a given position, compared to classical computers, which can analyze about a million possible moves. Quantum computers can crack encryption keys in a few minutes when classical computers would need over a thousand years. Hence Quantum Cryptography is of primary importance, since transactions over the Internet must be secure.
6. Conclusion
Many of the technological applications of Relativity Theory are already a reality. Nuclear fission has not yet reached technical maturity. Quantum Mechanics has led to the reality of lasers. But quantum information is still in a state of infancy. These technologies – nuclear fission and Quantum Information – have the potential to change the world. Some quantum technologies already prove to be extremely useful in the study of long-term environmental processes. For instance, analysis on the level of single atoms allows the dating of the age of water in the ocean and of ice in glaciers, thus providing important clues in the understanding of climate change.
Endnotes
[1] Lisa Randall, Knocking on Heaven’s Door: How Physics and Scientific Thinking Illuminate the Universe and the Modern World (London: The Bodley Head, 2011), 78.
[2] Amir D. Aczel, Entanglement: The Greatest Mystery in Physics (New York: Four Walls Eight Windows, 2002), 53.
[3] Anton Zeilinger, “Fundamentals of Quantum Information,” Physics World 11/3 (March 1998): 35.
[4] (Italics in original) Aczel, 68.
[5] Zeilinger, “Fundamentals of Quantum Information,” 36.
[6] Emerging Technology from the arXiv, “Einstein’s ‘Spooky Action at a Distance’ Paradox Older than Thought,” MIT Technology Review. https://www.technologyreview.com/2012/03/08/20152/einsteins-spooky-action-at-a-distance-paradox-older-than-thought/
[7] Wolfgang Tittel, Grégoire Ribordy, and Nicolas Gisin, “Quantum Cryptography,” Physics World 11/3 (March 1998): 41.
[8] Randall, 78.
[9] Aczel, 236-7.
[10] David Deutsch and Artur Eckert, “Quantum Computation,” Physics World 11/3 (March 1998): 48.
Further Reading:
Aczel, Amir D. Entanglement: The Greatest Mystery in Physics. New York: Four Walls Eight Windows, 2002.
Atkins, Peter. Galileo’s Finger: The Ten Great Ideas of Science. Oxford: Oxford University Press, 2003.
Deutsch, David. The Fabric of Reality. New York: Penguin Books, 1997.
Deutsch, David, and Artur Eckert. “Quantum Computation.” Physics World 11/3 (March 1998): 47-52.
Griffin, John. In Search of Schrödinger’s Cat: Quantum Physics and Reality. New York: Corgi Books, 1989.
Nielsen, Michael A. “Simple Rules for a Complex Quantum World.” Scientific American Special Edition: “The Edge of Physics” 13/1 (2003): 25-33.
Randall, Lisa. Knocking on Heaven’s Door: How Physics and Scientific Thinking Illuminate the Universe and the Modern World. London: The Bodley Head, 2011.
Rovelli, Carlo. Seven Brief Lessons on Physics. New York: Penguin Books, 2016.
Tegmark, Max, and John Archibald Wheeler. “100 Years of Quantum Mysteries.” Scientific American 284 (February 2001): 54-61.
Tittel, Wolfgang, Grégoire Ribordy, and Nicolas Gisin. “Quantum Cryptography.” Physics World 11/3 (March 1998): 41-45.
Zeilinger, Anton. “Fundamentals of Quantum Information.” Physics World 11/3 (March 1998): 35-40.
Zeilinger, Anton. “Quantum Teleportation.” Scientific American Special Edition “The Edge of Physics.” 13/1 (2003): 34-43.
Zeilinger, Anton. Dance of the Photons: From Einstein to Quantum Teleportation. New York: Farrar Straus Giroux, 2010.
*As noted in the Introduction, Digital pieces with *Guest Author in the title have been through the following process:
- Content editing by executive editor or ad hoc editor
- Peer Review with one reviewer
- Copyediting by executive editor

